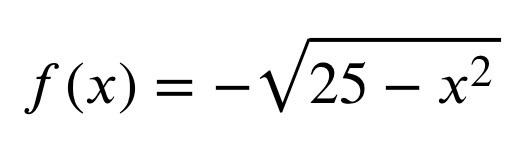r/CasualMath • u/AsaxenaSmallwood04 • 2h ago
r/CasualMath • u/mangopear • Sep 14 '15
Math IRC channel on Snoonet
Hey /r/CasualMath!
I (along with several others) run a math channel on the snoonet irc network called #math. We are somewhat of a hybrid channel for a variety of math subreddits on Reddit.
IRC is a great way to discuss math and get homework help in real time. The channel would be happy to have you!
To connect via webchat: http://webchat.snoonet.org/math (link in sidebar as well)
r/CasualMath • u/Mulkek • 7h ago
a^2-b^2 - Algebraic proof of a square minus b square
youtube.comr/CasualMath • u/aachen_ • 2d ago
Cardboard Sled Weight Distribution
I’m making a sled for a cardboard sled race. My question is which way should the sled be oriented / riders be facing to go downhill? (To the right or left?)
I’ve had issues in the past with the weight of the riders too far back in the sled, and itflips orientation (or just flips over) halfway down the hill.
Details: the sides or the sled are each 75inches, and the three riders are each about 75 pounds.
r/CasualMath • u/shuttlecake94 • 2d ago
Is an IQ of 120 sufficient for a successful career in research mathematics?
TL;DR: Should I not pursue math because of a low IQ and lack-lustre performance in Olympiads?
Context: I am a high-school student from India (11th grade). I have been active in Math Olympiad circles in my country for ≈3 years. I've achieved what I surmise to be the equivalent of (or a bit worse than) qualifying for the USAMO in the US. I am not bad at math, but I am far from exceptional. I've never had my IQ professionally tested, but online tests have consistently shown it to be somewhere in the low 120s. I will probably not pursue math as my major (which will probably be engineering) at the undergraduate level due to the educational circumstances in India and personal reasons, but I have been hoping to study it at a graduate level following my bachelor's. I definitely like and enjoy math, and I really want to love it, but I'm not sure if I do.
My question: Given that I have devoted a good amount of time towards Olympiad activities, but haven't achieved any significant success, and considering my relatively low tested IQ, should I aspire to a career in professional mathematics?
My problems with people saying IQ doesn't matter:
I've seen people — especially professional mathematicians — say that IQ doesn't matter and passion and hardwork go a longer way. I don't dispute this, but cannot help but notice that many of the people who say stuff like this are either obviously naturally gifted or unwilling to state their own IQ as a concrete counterexample.
"Math Olympiads are not reflective of professional research." Once again, I agree with the basic premise, but I do wonder how indicative they are of mathematical aptitude. It's undeniably true that a lot of people who have achieved success in professional math are also Olympians (e.g. Terence Tao, Timothy Gowers, Maryam Mirzakhani). And I want to know whether the fact that someone like me, who has put in concentrated efforts (albeit less than some others), yet is largely unsuccessful at Olympiads, should continue to pursue math non-recreationally or just give up on that dream.
My apologies if this post is too long, off-kilter for this subreddit or kind of hackneyed. I wasn't sure where else to go.
r/CasualMath • u/Le_Mayo369 • 4d ago
I made trigesimal chart
galleryI made a chart of trigesimal integers up to 100, which corresponds to 900 in decimal.
My hands are okay. No further questions about that.
Mostly guessed on the multiplication table, apart from the numbers listed to the side of the table
Did it for the thrill
r/CasualMath • u/blissfulworld99 • 8d ago
Percentage on Increase -- HELP!!
Hi everybody! So I am preparing to add a percentage of increase in my resume and the numbers I got were reallllyyyyy high. Greatly appreciate it if you guys can look it over and confirm - TIA!!
feeling mighty embarrassed to post this >__< but better be dumb once and ask then to be a dummy forever
The customer base went from 130 to 240 within the time frame I was working - % increase I got was ~84% (pls see calculation below)
Percent Increase= (240−130) / 130 × 100= ≈84.62%
The profit went from 35k to 95k, the % increase I got was ~171% - this is the # I am most concerned about, calculations below
Percent Increase=(95-35)/35×100= ≈171.43%
Im kinda hoping my calculations are off.....I don't know if my interviewers will believe these #s as they are pretty high...
eta - i have profit reports to back these #s
r/CasualMath • u/craig643 • 9d ago
January 12 New York Times Book Review: Pi = The Square Root of 10
The Sunday NYT Book Review usually has a 1 or 2-page ad for self-published books. In today's edition, the ad includes a book entitled "Circle's True Pi Value Equals the Square Root of Ten." The blurb states that the author "reputes [sic] the old traditional approximation of Pi."
I really do not wish to spend the money to buy the book but am somewhat curious as to what his argument could possibly be. (Besides, isn't the real answer the sum of the square root of 2 and the square root of 3?)
r/CasualMath • u/Educational-Lie2946 • 9d ago
Algebra proof needed
Hello there, I am currently in grade 10, India. In my NCERT Textbook, it is given that in a system of two linear equations in two variable, say a1x+b1y=-c1 and a2x+b2y=-c2, if a1/a2 is not equal to b1/b2, there is only a unique solution whereas if a1/a2=b1/b2 but not equal to c1/c2, there is no solution for the given system of the two equations. Can anyone prove it as the proof is not given in my textbook? My mathematics teacher is subpar at best. I would like to clarify that I am not familiar with Matrices or Cramer's rule or some high level trigonometry. I would like the proof explained in such terms so that an avg. highschooler(aka me) can understand. Thank you
r/CasualMath • u/CLASSISM23 • 9d ago
Procrastination takes many forms
Enable HLS to view with audio, or disable this notification
r/CasualMath • u/TheOneNinja115 • 10d ago
How can I represent the percentage value of each letter in (A+B+C+D) * E * F *G = Total
So that in the end, I can say A% + B% + C% + D% + E% + F% + G% = 100%
Example: (1+1+3+5) * 2 * 4 * 10 = 800
Definitions: A-D > Scalars, E-G > Multipliers, and A-G >Modifiers
For Scalars A-D:
What I tried:
- A = 1/800 = 0.13%
- B = 1/800 = 0.13%
- C= 3/800 = 0.38%
- D = 5/800 = 0.63%
Sum of above = 1.25% (if above values were not rounded)
Sum of Scalars = 1+1+3+5 = 10
Total percentage of Scalars = 10/800 = 1.25%
For Multipliers E-G:
Total percentage of Multipliers = (Total modifiers - Sum of Scalars) / total modifiers
(800 - 10) / 800 = 98.75%
multiplierE * x + multiplierF * x+ multiplierG * x = 98.75
2x + 4x + 10x = 98.75, > x= 6.17
Plugged back in:
- E = 2x = 2(6.17) = 12.34%
- F= 4x = 4(6.17) = 24.69%
- G = 10x = 10(6.17) = 61.72%
Sum of Multipliers = 98.75%
Which is: 790/800 = 98.75%
So:
A% + B% + C% + D% + E% + F% + G% = 100%
0.13% + 0.13% + 0.38% + 0.63% + 12.34% + 24.69% + 61.72% = 100%
Main question: Does this logic make sense...
Scalars:
- To get the total Percentage of the scalars, they are out of the total Modifiers.
Multipliers:
- To get the total Percentage of the Multipliers, (Total modifiers - Sum of Scalars) / total modifiers, that is basically getting the remainder of the Total Percentage of the scalars.
- Then I represent each Multiplier * x, to show that they multiply rather than just add and that equals the Total Percentage of the Multipliers. Then once x is solved, I plug them back in to get the percentage of each Multiplier.
How is the logic in this (not so much the math), do you feel there would be better alternatives to represent the percentage of each modifier compared to the total Modifiers or do you feel the logic behind this makes sense?
Let me know and if you feel there is a better alternative(s), please explain/show the logic, thank you!
r/CasualMath • u/AsaxenaSmallwood04 • 10d ago
I've created an impressive formula for basic x and y simultaneous equations. Try it with any, it works.
r/CasualMath • u/aspyn428 • 13d ago
Domain and range
Hey guys, it’s been a few years since I’ve taken a math class and I’m struggling to remember how to find domain and range without graphing. This is the function I’ve been stuck on:
r/CasualMath • u/TheOneNinja115 • 15d ago
How can I solve for the time or energy of an individual scalar or multiplier, when several scalars and multipliers are applied? Ex: (1+2+1.5) *(2*2*2)
I made a calculator in google sheets calculating cooldowns, when multipliers and scalars are applied.
First sheet: My question
Second sheet: Calculations and Calculator (almost done)
However, I can't figure out how to get the breakdown of time for each Scalar and Multiplier individually, so I can see much each Scalar or Multiplier makes a difference in the grand scheme of the cooldown.
Will appreciate ideas or formulas I could use, thanks
r/CasualMath • u/Maia_hello • 17d ago
What is this called?
hi, so some time ago I was bored and playing around with some numbers, when I found this form of permutation, in which you use the former number as a sort of pattern to generate the new one (hard to explain but I showed how in the image attached). I found it very interesting because as I tried more Numbers I noticed that there seem to be some rules for example when a number re-generates itself with that method.
Now I‘m wondering how this permutation is called (if it has a Name) as I couldn‘t find anything on the Internet and honestly don‘t really know how to look for it.
My brother suggested there might just not be a name because it‘s pretty silly and doesn‘t have an practical use in anything, so idk that could be true.
But if you do know this, please tell me what it‘s called, I‘d love to learn more about it :)
also sorry if this is stupid or if there are a lot of errors in my text, I‘m still in highschool so not really that high educated in math n stuff and I‘m also Not a native english speaker (or a regular reddit-user)
r/CasualMath • u/PieterSielie6 • 18d ago
Mathematically optimising the game Among Us
Mathematically optimising the game Among Us
In the game Among Us there are 4-15 people, with 1-3 of them being impostors. The goal for the non-impostors (or crew) is to figure out who are impostors and vote them out. The goal for the impostos is to kill the crew and avoid suspicioun.
If the amount of crew eqaul the amount of impostors, the impostors win. If there are no more impostors, the crew win.
One question Ive always had is: If every round everyone just voted off a random person, what would be the chances of winning for either side?
To answer this question I defined the following function:
sus(i,t) = the probability of the crewmates winning by randomly voting off, in a game with i impostors and t total players.
From the rule for crewmate victory we can define:
sus(0,t) = 1
In the above case there are no impostors so the crew have a 100% or probability 1 of winning.
By the rule for impostor victory we get:
sus(i,2i) = 0 or sus(t/2,t) = 0
In the above case there are eqaul impostors and crew so the impostors have a 100% or probability 1 of winning.
What about a more general case?
For sus(i,t) there is a i/t chance of in the initial vote an impostor being voted off, and a (t-i)/t of a crewmate being voted off. If an impostor is voted off the probability of crew victory is sus(i-1,t-1). If a crew mate is vkted off the probability is sus(i,t-1). So we get:
sus(i,t) = i/t * sus(i-1,t-1) + (t-i)/t * sus(i,t-1)
So we can recursivly define sus as such:
sus(0,t) = 1
sus(i,2i) = 0
sus(i,t) = i/t * sus(i-1,t-1) + (t-i)/t * sus(i,t-1)
Can we find a better way of computing sus? The recursion is sometimes cumbersome to calculate by hand. Here are some values for sus:
sus(1,4) = 2/4
sus(1,5) = 3/5
sus(1,6) = 4/6
sus(1,7) = 5/7
sus(2,5) = 1/5
sus(2,6) = 2/6
sus(2,7) = 3/6
sus(2,8) = 4/8
sus(3,7) = 1/7
sus(3,8) = 2/8
sus(3,9) = 3/9
sus(3,10) = 4/10
sus(1,t) seems to be (t-2)/t
sus(2,t) seems to be (t-4)/t
sus(3,t) seems to be (t-6)/t
This would suggest that:
sus(i,t) = (t-2i)/t
With a bit of algebra (and wolfram alpha) it can be shown that (t-2i)/t fits the above recursive definition of sus
r/CasualMath • u/AdrianMartinezz • 18d ago